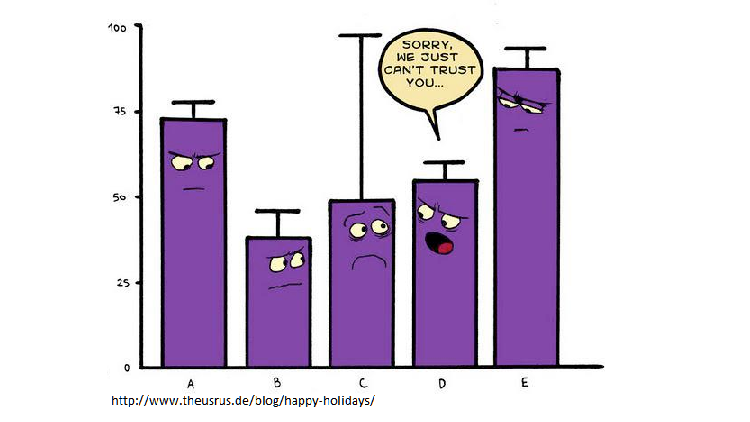
Personal ja mõõtmine - usalduspiirid
Eelmises artiklis rääkisime, miks töötajate pühendumuse ja rahulolu uurimisel tuleb võrrelda oma tulemusi võrdlusgrupiga. Käesolevas postituses keskendume sellele, kuidas oleks kõige õigem küsitlustulemusi omavahel võrrelda. Teema sissejuhatuseks sobib väga hästi päris mitme meie kliendi suust kõlanud küsimus:
Tavaliselt kõik inimesed küsitlusele ei vasta. Öelge, milline peab olema vastamismäär selleks, et võiksime lugeda uuringu tulemusi usaldusväärseks?
Seega tundub, et kõhutunde järgi saavad paljud inimesed aru – kui kõik küsitletavad küsitlusele ei vasta, siis on küsitluse abil kogutud informatsioon puudulik. Samas näitab meie kogemus, et sageli peetakse selle „puudulikkuse“ täpsemat lahtimõtestamist liiga keeruliseks ning lõppkokkuvõttes otsustatakse seda probleemi sageli lihtsalt ignoreerida. See on aga üks suuremaid vigu, mida küsitlusuuringu tulemuste tõlgendamisel teha saab. Kohe seletamegi ühe lihtsa näite najal veidi lähemalt, milles see viga seisneb ja miks on nii oluline selliseid vigu vältida.
Kujutame ette olukorda, et meil on finantsosakonnas 10 inimest ja me palusime neil 5-pallisel skaalal hinnata rahulolu oma tööga. Meie küsimustikule vastas 5 inimest, kelle keskmine rahulolu oma tööga oli 3,2. Kui meid huvitaks ainult nende inimeste arvamus, kes küsimustikule vastasid, siis oleks kõik väga lihtne – 3,2 ongi selle grupi hinnang oma tööga rahulolule. Kui võrdlusgrupis oli küsitlusele vastanute keskmiseks hindeks 3,0, siis võimegi sellest järeldada, et puhtalt küsitlusele vastanuid võrreldes on finantsosakond oma tööga rohkem rahul kui võrdlusgrupp.
Probleem seisneb selles, et enamasti ei huvita meid ainult küsitlusele vastanute arvamus. Me tahame teada kõigi selles üksuses töötavate inimeste arvamust. Olgu öeldud, et kõigi küsitletavate käest vastust saamata on võimatu öelda, milline see täpselt on. Küll aga suudame me matemaatilisele statistikale tuginedes öelda, millisesse vahemikku võiks kõigi üksuse töötajate arvamus suure tõenäosusega jääda. Seda vahemikku nimetatakse usaldusvahemikuks, mida ilmestatakse joonistel usalduspiiridega. Sotsiaalteaduses kasutatakse sageli 95% usalduspiire, mis näitavad, et kui me saaksime korraldada seda uuringut 100 korda järjest ja vastama satuksid iga kord veidi erinevad inimesed, siis 95 juhul 100-st jääb kõigi üksuse töötajate arvamus usalduspiiride alumise ja ülemise otsa vahele. Sisuliselt näitavad usalduspiirid seda, kui kindlad me oma uuringus esitatavates andmetes oleme – mida kitsamad on usalduspiirid, seda täpsemalt me teame, milline töötajate pühendumus või rahulolu on.
Usalduspiire peljatakse sageli seetõttu, et usaldusvahemikest on natuke ebamugavam rääkida kui punkthinnangutest – ühe numbri (keskmine) asemel tuleb ära tuua kaks (ülemine ja alumine usalduspiir). Kui panna see info aga joonisele, siis on kõik väga lihtne (vt joonist 1), sageli ei ole usalduspiiride numbriliste väärtuste kasutamine isegi vajalik.
Tuleme veelkord tagasi meile juba tuttava finantsosakonna juurde. Kui tahame 95% kindlusega öelda, et kasutame õigeid näitajaid, siis pole meil mingit põhjust arvata, et finantsosakonna kui terviku keskmine tööga rahulolu on võrdne just küsitlusele vastanute hinnangute keskväärtusega (tähistatud joonisel täpiga) – tegelikkuses on see suvaline punkt usalduspiiride alumise ja ülemise otsa vahel. Kui võrrelda seda vahemikku võrdlusgrupi omaga, siis saab ilmseks, et finantsosakonna tööga rahulolu võib olla nii kõrgem kui madalam võrdlusgrupist – kui aus olla, siis me lihtsalt ei tea. Olukord on hoopis teistsugune aga turundusosakonna puhul, kus on selge, et töötajate tööga rahulolu on võrdlusgrupi omast kõrgem. Loomulikult on kahe näitaja statistiliselt olulise erinevuse testimiseks komplitseeritumaid meetodeid, kuid usalduspiiride võrdlemine annab meile suurusjärguliselt õige pildi kätte.
Joonis 1. Tööga rahulolu (keskmine vastuste skoor 5-pallisel skaalal)
Hakkame otsi kokku tõmbama. Kui uuringu tulemused on ebatäpsed (ja küsitlusuuringute puhul nad alati on), siis tuleb seda ka ausalt välja öelda. Vastasel juhul on väga tõenäoline, et anname ettevõtte juhtkonnale halba nõu. Antud näite puhul oleks vale järeldada, et nii finants- kui turundusosakonna näitajad on väga head. Finantsosakonna tulemusi oleks tõenäoliselt mõistlik veidi põhjalikumalt edasi uurida. Kui teil oli plaanis maksta finantsosakonna juhile tulemustasu selle eest, et ta on suutnud luua oma meeskonnas võrdlusgrupist parema tööõhkkonna (mõõdetuna läbi töötajate tööga rahulolu), siis on küllaltki tõenäoline, et te maksate seda olukorras, kus tulemustasu saamine ei ole tegelikult õigustatud.
Järgmises postituses mõtiskleme selle üle, kas statistiliselt oluline erinevus tähendab ühtlasi ka sisuliselt olulist erinevust ning miks on sisulise olulisuse hindamine sageli keerulisem kui esmalt paistab.
PS. Olgu igaks juhuks mainitud, et tegelikkuses on ebakindluse allikaid rohkem kui ainult madal vastamisaktiivsus. Näiteks ei tea me, kui hästi peegeldab meie poolt küsitud küsimuse vastus seda, mida me päriselt teada tahtsime – äkki said vastajad küsimusest hoopis teist moodi aru, kui meie? Piirdume praegu mittevastamise mõju arvesse võtmisega ja tuleme teiste veaallikate juurde tagasi hilisemates postitustes.

